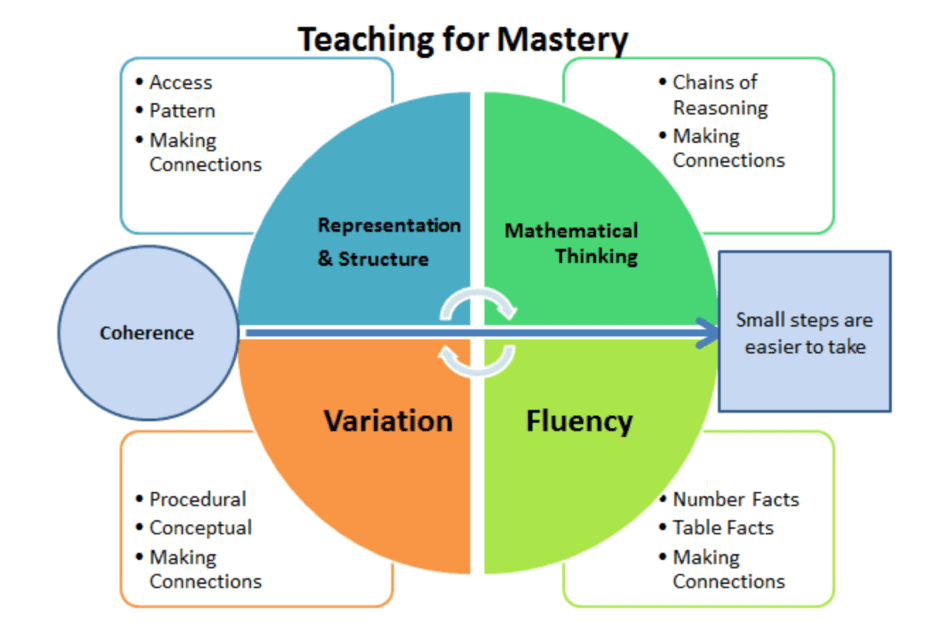
Fluency in Mathematics
One of the three aims of the KS3 National Curriculum for Mathematics aims is to ensure that all students:
· become fluent in the fundamentals of mathematics, through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately. This is also one of the 5 big ideas of mastery.
Fluency rests on a well-built mathematical foundation with three parts:
1. An understanding of the meaning of the operations and their relationships to each other, for example, the inverse relationship between multiplication and division;
2. The knowledge of a large repertoire of number relationships, including the addition and multiplication facts, as well as other relationships (for example, how 4 x 5 helps us to work out 4 x 50 with understanding);
3. A thorough understanding of the base ten number system, how numbers are structured in this system and how the place value system of numbers behaves in different operations, for example 24 + 10 = 34 and 24 x 10 = 240.
England Are Fabulous
Fluency relies on three main ideas:
Efficiency
Accuracy
Flexibility
So what does it look like in our classrooms?
I asked my year 7 class to do this calculation on their mini-whiteboards:
7002 – 1999
Every student went straight to the column method for subtraction and the results were varied.

As you can see, the correct answer is 5003, but is this the most efficient way?
We know that £10 – £5 gives us the same answer if we do £11 – £6.
For the calculation above, a more efficient method would have been:
7003 – 2000 = 5003 or maybe using the number line to ‘add on’.
Many students are faced with calculation problems involving money such as:
£10 – £1.93. In my experience, many students would do 10.00 – 1.93 as a column subtraction and get ‘stuck’ with borrowing, however, if they did 9.99 – 1.92, there would be no borrowing in their calculation. Alternatively, they could use the ‘add on’ method.
These are just a few examples. The mathematics department are now building into their KS3 curriculum ‘calculating smartly’ lessons.
Can you do these calculations ‘smartly’?

Mrs S Bennett (Teaching for Mastery Lead for Abacus NW Maths Hub)









